Standard Deviation Calculator
Enter comma-separated values (e.g., 10, 12, 23, 23, 16, 23, 21, 16):
In statistics, the standard deviation, usually represented by σ, is a measure of variance or dispersion (the degree to which a distribution is stretched or squeezed) between values in a collection of data. The data points tend to be closer to the mean (or expected value), μ, when the standard deviation is lower. On the other hand, a larger range of values is indicated by a bigger standard deviation.
Like other statistical and mathematical ideas, standard deviation can be applied in a wide range of contexts and, consequently, in a wide range of equations. The standard deviation is frequently used to quantify statistical outcomes like the margin of error in addition to representing population diversity. When applied in this way, The standard deviation is frequently referred to as the standard error of the estimate with respect to a mean or the standard error of the mean. In addition to calculating sample and population standard deviations, the calculator above also approximates confidence intervals.
Standard Deviation of the Population
When the entire population can be measured, the population standard deviation, or σ, is defined traditionally as the square root of the variance of a specific data set. The following formula can be used to determine the population’s overall standard deviation when it is feasible to sample every member of the population:
The equation above may appear intimidating to individuals who are not familiar with summation notation, but it is not a particularly complex summation when broken down into its component parts. The starting index is indicated by the i=1 in the summation; for the data set 1, 3, 4, 7, 8, i=1 would be 1, i=2 would be 3, and so forth. Because there are five values in this data set, the summation notation simply means to apply the operation of (xi – μ)2 to each value through N, which in this case is 5.
For example: μ = (1+3+4+7+8) / 5 = 4.6 σ = √[(1 – 4.6)2 + (3 – 4.6) Two plus… plus (8-4.6)2)] 5.76 + 11.56 + 0.36 + 12.96 + 2.56 + √(12.96 + 2.56)/5 = 2.577
Standard Deviation of a Sample
Since it is frequently impossible to sample every member of a community, the aforementioned equation must be changed in order to calculate the standard deviation using a random sample of the population under study. Usually represented by s, the sample standard deviation is a popular estimator for σ.It should be noted that there are numerous formulas for determining sample standard deviation since, in contrast to sample mean, sample standard deviation lacks a single estimator that is objective, effective, and has a maximum likelihood. Below is the formula for the “corrected sample standard deviation.”
It is a corrected version of the equation that eliminates some of the bias in the equation by adjusting the population standard deviation equation to use the sample size as the population size. However, unbiased standard deviation estimation is very complex and changes according to the distribution.Because of this, the “corrected sample standard deviation,” also known as just the “sample standard deviation,” is the most widely used estimator for population standard deviation. For small sample sizes (N<10), it still has a large bias, but it is a far better approximation than its uncorrected form.
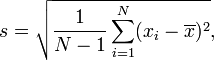
One example value is wherexi.
x̄ represents the sample mean.
The sample size is N.
For a sample of working with summaries, see the “Population Standard Deviation” section. With the exception of the N-1 term in the corrected sample deviation equation and the application of sample values, the equation is nearly identical.
Uses for Standard Deviation
In both industrial and experimental contexts, standard deviation is frequently used to compare models to actual data. Quality control for certain products is one instance of this in industrial settings. A minimum and maximum value that a certain feature of the product should fall within a high percentage of the time can be determined using the standard deviation. To maintain quality control, adjustments to the production process could be required when values deviate from the computed range.
In meteorology, standard deviation is often used to identify regional climate variations. Assume that the mean temperature of two cities, one deep inland and one on the coast, is 75°F. Although this could lead one to assume that the temperatures in these two cities are nearly same, if the mean is the only factor considered and the standard deviation is disregarded, the truth may be obscured. Since water has a higher heat capacity than land,
coastal towns typically experience much more stable temperatures because of the regulation provided by huge bodies of water. In other words, coastal areas stay warmer in the winter because water is less sensitive to temperature variations.and colder in the summer because of the energy needed to adjust the water’s temperature. Therefore, an inland city may experience temperatures ranging from 30°F to 110°F to produce the same mean, whereas a coastal city may experience temperature variations between 60°F and 85°F during a given length of time to produce a mean of 75°F.
Standard deviation is also widely utilized in the finance industry, where it is frequently employed to quantify the risk involved in changes in the price of an asset or portfolio of assets. In these situations, the standard deviation is used to evaluate the degree of uncertainty surrounding prospective returns on a particular investment..
Stock A, which has an average return of 7% with a standard deviation of 10%, would obviously be the safer choice when compared to stock B, which has the same average return but a standard deviation of 50%. This is because stock B’s standard deviation is much higher for the same return. Because standard deviation can skew the mean in either direction, this does not prove that stock A is a better investment choice in this particular situation. Stock B may offer a substantially bigger return (or loss), but Stock A is more likely to have an average return that is closer to 7%.
There are several applications for standard deviation; these are only a handful. In general, standard deviation is useful if one wants to know how much a typical value from a distribution can deviate from the mean.